

So by calling move, the effect is A - 1, B + 1.

However I believe this should help explain thing (I did this by hand so it could be wrong, sorry too lazy load up the project on my java computer).Ĭonsider Move(2, A=0, B=1, C=2) (C(0) = 3, count of stack 0.I gave it 3 so I could use it later on) Let’s look at the output.Well if I had to recommend, I would say put the debugger on the move, and look at how it flows, and you should be able to track down the null pointer. Lastly, it prints the elements of the destination stack to see whether our output is correct. It prints the top element of the stack to which the disk was transferred as that disk is now the top element of that stack. The main() function prints the number of the disk that was transferred and the name of the poles from and to which it was transferred. The main() function divides the problem into two cases as mentioned above(n=odd number and n=even number) and calls the transfer_disk() function according to the corresponding transfers of the two cases, also as mentioned above. This is how the transfer of the top element from one stack to the other is ensured to be valid. If neither the stacks are empty it compares the top element of both and pushes the smaller one of the two into the stack which has the bigger top element. The function checks if either of the two stacks are empty and pushes the top element of the one which is not empty into the one which is empty. The transfer_disk() function takes two parameters by reference so that the changes made to them are reflected in the main program. Let’s understand the transfer_disk() function first to see how we have implemented the valid transfer of disks. We create three integer stacks named s,a and d(source, auxiliary and destination poles) and take the input n, for the number of disks. While(i to implement stack in this problem.
Hanoi towers visualzier code#
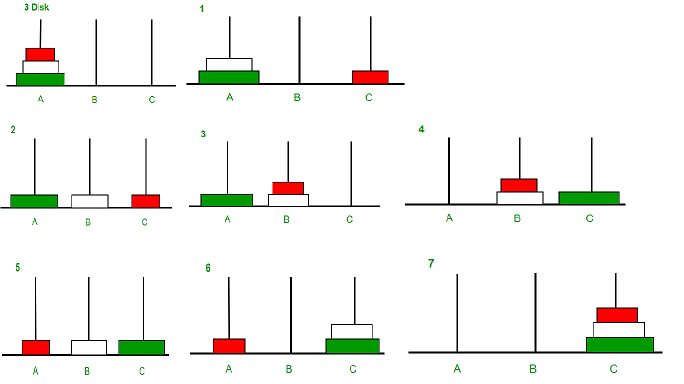
Now that you have understood the approach, let’s take a look at the code to understand how exactly stack implementation of Tower of Hanoi takes place- #include It is not possible to place a larger disk on top of a smaller disk. Std::to_address in C++ with example C++ Program: Tower of Hanoi using stackĪn important point that we have to consider while writing our code is that this transfer should be a valid transfer i.e. This implies that we can iteratively implement Tower of Hanoi using stacks in C++. Similarly for n being an even number the 3 transfers being repeated in an order are-ġ) First transfer between source and destination poleĢ) Second transfer between source and auxiliary poleģ) Third transfer between destination and auxiliary pole We notice that for n being an even number, there are 3 transfers being repeated in an order-ġ) First transfer between source and auxiliary poleĢ) Second transfer between source and destination poleģ) Third transfer between auxiliary and destination pole The second step is to make two cases, one for n being an even number and the other for n being an odd number. So we notice that for a number of disks, n, it takes us 2^n-1 steps. Similarly, If we solve for n=3, we find that it takes 7 steps to move all three disks from the source. Solving for n=2, first we move disk 1 from the source to the auxiliary pole, then disk 2 from the source to the destination pole and at last disk 1 from the auxiliary to the destination pole taking us a total of 3 steps. The way to go about this problem is to first take examples with n being a very small number. The problem and the goal for n=3 looks like this The objective is to move the disks from the source pole to the destination pole according to the following rules-Ģ) You cannot place a larger disk on top of a smaller disk. the disk numbered 1(smallest disk) is on the top of the stack. The disks are first on the source pole in a descending order from bottom to top i.e. The size of the disk is directly proportional to the number on it and the three poles are known as source pole, auxiliary pole and destination pole. Tower of Hanoi is a very famous puzzle that involves disks numbered from 1 to a number n and three poles. Let’s first understand the problem and it’s rules.
Hanoi towers visualzier how to#
In this tutorial, we will learn how to solve Tower of Hanoi using stack in C++.


 0 kommentar(er)
0 kommentar(er)
